 Plan d’expérience
Plan d’expérience
Yrelay vous propose un exemple simple de la méthodologie du plan d’expérience.
Considérons un marchand de téléviseurs.
Il souhaite mettre en oeuvre un plan d’expérience pour diminuer le nombre de défauts au cours de son procédé de brasage.
Il faut tout d’abord définir "ce que l’on veut mesurer" :
dans notre exemple : ce sera la moyenne des défauts constatés sur des lots de 20 soudures observées.
On appellera cela la réponse Y.
Il faut ensuite lister les facteurs pouvant influencer le nombre de défauts ainsi que leurs valeurs mini et maxi (notées par les symboles -1 ou +1) :
dans notre exemple il y en a 3 :
– facteur A : température du bain variant entre 229°C et 234°C
– facteur B : température de préchauffe variant entre 140°C et 160°C
– facteur C : hauteur de la vague sur buse variant entre 8 mm et 10 mm
Il faut réaliser 2 puissance n facteurs = 2exp3 = 8 expériences différentes.
Les 8 expériences différentes se contruisent ainsi :
– 1ère expérience : les 3 facteurs A, B, C prennent leur valeur mini
– 2ème expérience : le facteur A prend sa valeur maxi et B et C leurs valeurs mini
– 3ème expérience : le facteur A prend sa valeur mini, B sa valeur maxi et C sa valeur mini
et ainsi de suite.
Ces 8 expériences peuvent ainsi se représenter par une matrice "immuable" :
| N° exp. | Valeur A | Valeur B | Valeur C |
|---|---|---|---|
| 1 | x11 = -1 | x12 = -1 | x13 = -1 |
| 2 | x21 = +1 | x22 = -1 | x23 = -1 |
| 3 | -1 | +1 | -1 |
| 4 | +1 | +1 | -1 |
| 5 | -1 | -1 | +1 |
| 6 | +1 | -1 | +1 |
| 7 | -1 | +1 | +1 |
| 8 | +1 | +1 | x83 = +1 |
On va "améliorer" cette matrice en rajoutant des colonnes supplémentaires à l’aide des formules suivantes :
– la colonne I (moyenne du plan) est par définition toujours égale à +1
– AB = valeur A * valeur B
– AC = valeur A * valeur C
– BC = valeur B * valeur C
– ABC = valeur A * valeur B * valeur C
– Y = résultats des expériences
| Exp | I | A | B | C | AB | AC | BC | ABC | Y |
|---|---|---|---|---|---|---|---|---|---|
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 10 |
| 2 | +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 7.6 |
| 3 | +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 11 |
| 4 | +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 7.6 |
| 5 | +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 6.2 |
| 6 | +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 7.1 |
| 7 | +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 6.3 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 7 |
On calcule ensuite les deux formules suivantes :
– I (Moyenne du plan) = Somme des réponses Y / Nombre d’expériences
– I = (10 + 7.6 + 11 + 7.6 + 6.2 + 7.1 + 6.3 + 7) / 8 = 7.85
– Ej (Influence du facteur j) = Somme des xij * Y / Nombre d’expériences
– Influence du facteur A = [(-1)*10 + (+1)*7.6 + (-1)*11 + (+1)*7.6 + (-1)*6.2 + (+1)*7.1 + (-1)*6.3 + (+1)*7] / 8 = - 0.525
– Influence de la simultanéité facteurs A et C = [(+1)*10 + (-1)*7.6 + (+1)*11 + (-1)*7.6 + (-1)*6.2 + (+1)*7.1 + (-1)*6.3 + (+1)*7] / 8 = 0.925
Et ainsi de suite : en ajoutant le résultat des coefficients d’influence sur la première ligne : la matrice est désormais complète :
| Exp | I | A | B | C | AB | AC | BC | ABC | Y |
|---|---|---|---|---|---|---|---|---|---|
| E | 7.85 | -0.525 | 0.125 | -1.2 | -0.15 | 0.925 | -0.125 | 0.1 | . |
| 1 | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 10 |
| 2 | +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 7.6 |
| 3 | +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 11 |
| 4 | +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 7.6 |
| 5 | +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 6.2 |
| 6 | +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 7.1 |
| 7 | +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 6.3 |
| 8 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 7 |
On réalise ensuite un diagramme de Pareto avec les valeurs absolues des coefficients d’influence afin de déterminer les effets les plus forts :
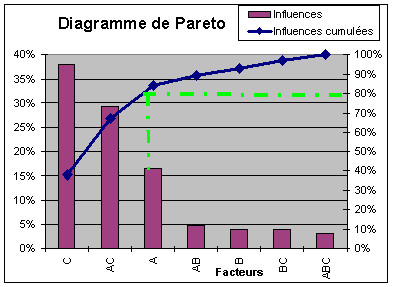
Ainsi, les facteurs les plus influents sont : C ; l’interaction AC et enfin A.
Les autres facteurs et interactions sont non-significatifs.
Il faut ensuite étudier de plus près le sens de l’influence des facteurs C ; AC et A.
Pour cela : nous utilisons une méthode graphique.
Lors des 8 expériences, lorsque le facteur C a sa valeur minimale (-1), les résultats sont : Y = 10 ; 7.6 ; 11 ; 7.6 soit une moyenne de (10 + 7.6 + 11 + 7.6) / 4 = 9.05
Lors des 8 expériences, lorsque le facteur C a sa valeur maximale (+1), les résultats sont : Y = 6.2 ; 7.1 ; 6.3 ; 7 soit une moyenne de (6.2 + 7.1 + 6.3 + 7) / 4 = 6.65
On dit que le nombre de défauts évolue linéairement en fonction du facteur C de la façon suivante (on a également représenté la moyenne des défauts I = 7.85) :
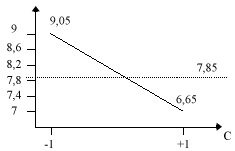
On représente également l’évolution du nombre de défauts en fonction de l’interaction AC et du facteur A :
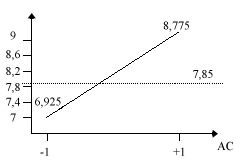
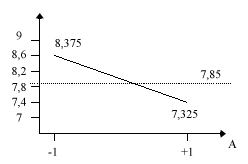
Conclusion :
L’objectif est de minimiser le nombre de défauts (Y).
Pour cela, on va régler les facteurs par ordre décroissant d’effet.
Ainsi, dans notre exemple, on va effectuer les réglages suivants :
– Il faut régler le facteur C au maximum de sa valeur
– Il faut régler l’interaction AC au minimum de sa valeur : C est déjà au maxi, donc on règle A au minimum.
Soit enfin le paramétrage optimal :
– C = 10 mm
– A = 229°C
– B est "indifférent"
Dans l’exemple que nous venons de décrire : les facteurs A, B et C sont dits "discontinus" puisqu’ils peuvent prendre soit une valeur minimale soit une valeur maximale.
Supposons désormais que l’on souhaite travailler avec des facteurs "continus", on peut modéliser la réponse Y de la façon suivante :
Y = I + Eaxa + Ebxb + Ecxc+ Eabxaxb + Ebcxbxc + Eacxaxc + Eabcxaxbxc
Si l’on ne retient que les facteurs influents C ; AC et A :
Y = 7.85 + Ecxc + Eacxac + Eaxa
Y = 7.85 - 1.2 * xc + 0.925 * xa * xc - 0.525 * xa
avec :
– xa = [A(°C) - (min + max)/2] / (max - min)/2
– xa = [A(°C) - (229 + 234)/2] / (234 - 229)/2
– xa = (A(°C) - 231.5)/2.5
– xc = [C(mm) - (min + max)/2] / (max - min)/2
– xc = [C(mm) - (10 + 8)/2] / (10 - 8)/2
– xc = C(mm) - 9
Y = 7.85 - 1.2 * xc + 0.925 * xa * xc - 0.525 * xa
Y = 7.85 - 1.2*[C - 9] + 0.925*[(A-231.5)/2.5]*(C - 9) - 0.525*[(A-231.5)/2.5]
Y = 752.505 - 86.855 * C(mm) + 0.37 * A(°C) * C(mm) - 3.54 * A(°C)
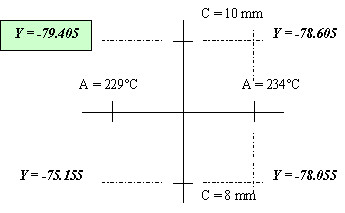
On vérifie bien que le nombre de défauts Y prend sa plus petite valeur (-79.405) pour le paramétrage :
– C = 10 mm
– A = 229°C
et sa plus grande valeur pour le paramétrage :
– C = 8 mm
– A = 229°C
Cet article a été rédigé à partir des liens suivants :
– http://fr.wikipedia.org/wiki/Plan_d’exp%C3%A9rience
– http://www.cyber.uhp-nancy.fr/demos/QUAL-004/cha_2/cha_2_9_3.html
 Yrelay.com
La planète de la communauté !
Yrelay.com
La planète de la communauté !